Liquid Crystals Physics Group
My studies concern one- and two-dimensional deformations of director field as well as changes of optical transmision of liquid crystal layers. Effects of this kind are fundamental for every application of liquid crystals.
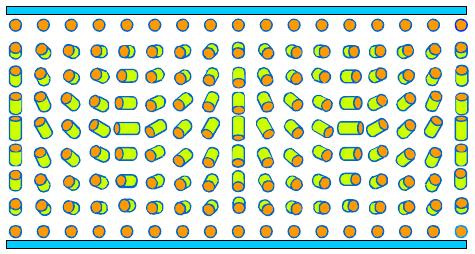
Structure of
two-dimensional domains in nematic layer.
Numerical models used for simulations are based on continuum theory which is very well confirmed by experiments.
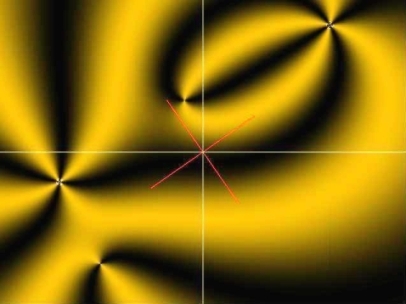
Schlieren
texture of nematic layer.
Simulations concern static structures as well as dynamics of them. They take into account the charge transport in nematic material and flows of nematic liquid connected with deformations.
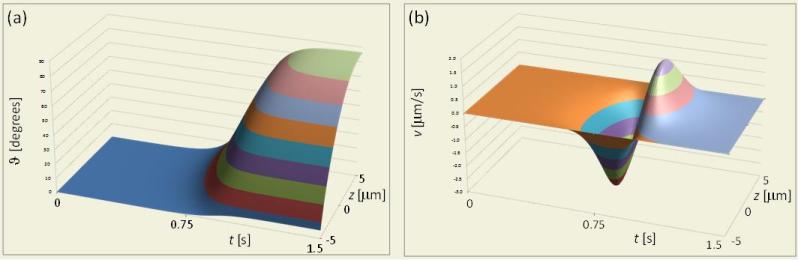
Director
distribution and flow velocity distribution during onset of deformation of
nematic layer.
M. Buczkowska, G. Derfel, “Backflow in flexoelectric nematic layers deformed by electric field”, Liquid Crystals, 42, (2) 169-175 (2014)
The aim of my numerical simulations is to find out what is the influence of parameters (e.g. dielectric anisotropy, flexoelectricity, ion concentration, anchoring strength) on elastic, rheological, electrical and optical properties of nematic layers.
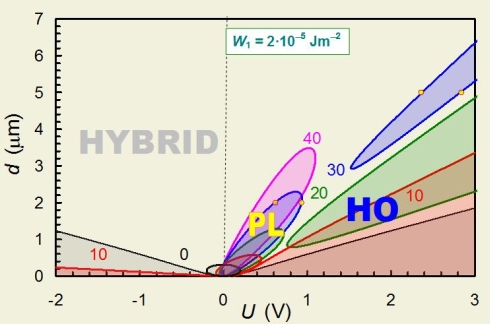
Ranges of
existence of planar, homeotropic and hybrid structure in layers of nematics
possessing various flexoelectric coefficients.
G. Derfel , “Stationary states of hybrid aligned flexoelectric nematic layers”, Liquid Crystals, 34, (10) 1201-1214, (2007)
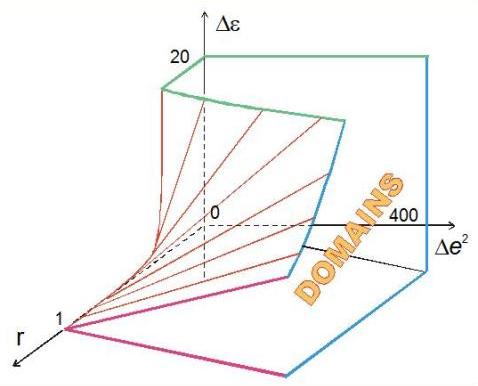
Region of
existence of two-dimensional domains in parameters space characterizing dielectric, flexoelectric and elastic properties.
G. Derfel, M. Buczkowska, “Numerical study of flexoelectric longitudinal domains”, Molecular Crystals and Liquid Crystals, 547, 213-221, ( 2011)
Group Leader
Recent Publications
-
M. Szmigielski, Stability conditions of a twist-bend nematic phase according to Barbero's theory, Phys. Rev. E 108(1), 014701, 2023
-
M. Szmigielski, Theoretical models of modulated nematic phases, Soft Matter 19(15), 2675-2704, 2023
-
M. Buczkowska, Influence of Parameters on Flexoelectro-Optic Effect in Cholesteric Liquid Crystals, Acta Phys. Pol. A 140(3), 258-264, 2021
-
M. Buczkowska, Spatially periodic deformations in hybrid aligned flexoelectric nematic layers, Liq. Cryst. 49(2), 277-282, 2021
-
M. Buczkowska, J. Graczykowski, Spatially periodic deformations in super-twisted flexoelectric nematic layers, Liq. Cryst. 48(3), 436-440, 2020



